2025-09-05 3931 0
高陡岩质边坡低倾角裂缝三维连通性计算方法
3D connectivity calculation method for low-dip fractures in high-steeprock slopes

摘要:
低倾角裂缝是控制高陡岩质边坡稳定性的主要裂缝之一,直接影响拱坝坝肩的抗滑稳定性。岩体中裂隙的空间复杂性和随机性给三维连通性的精确测定带来了挑战。本文提出了一种计算三维连通性的新方法。通过修正裂缝与测量窗口夹角造成的采样偏差,采用基于copula的二元分布模型对裂缝产状进行建模,构建了能准确反映裂缝空间分布的三维离散裂缝网络(DFN)模型。采用最优路径搜索算法(A*算法)识别DFN模型中不同断面的潜在破坏路径,并采用离散插值分析预测不同高程下的潜在三维剪切面。然后使用布尔运算将涉及穿透破坏的裂缝投影到三维表面上,最终获得反映工程岩体破坏模式的三维连通性。应用该方法对西藏某水电工程坝肩岩体低倾裂缝连通性进行了评价。数值仿真结果验证了该方法的准确性。此外,通过与传统二维方法的对比分析,进一步验证了所提出的三维连通率计算方法的可靠性。本文为水电工程坝肩岩体的抗滑稳定性和地基面的选择提供了参考,并对岩体裂隙的三维连通性特征有了新的认识。
引言:
裂缝,也称为节理,是沿应力导致岩石局部失去凝聚力的平面,通常两侧岩石都没有明显的位移。随机分布的裂隙对控制岩体的基本力学行为和整体稳定性起着至关重要的作用。它们不仅影响岩体的强度,而且是工程失稳的潜在几何和力学边界。在实际工程中,岩体抗剪强度问题往往涉及节理和岩桥的联合抗剪强度,这在很大程度上依赖于沿潜在破坏面断裂连通性的准确计算。特别是在高陡岩质边坡的稳定性分析中,低倾角裂缝的连通性特征对坝肩岩体的抗滑稳定性评价起着关键作用
低倾角裂缝是构成边坡运动的主要构造面之一,其连通性直接影响岩体的整体强度和稳定性。然而,由于岩体中裂缝发育的空间复杂性和随机性,以往的研究人员发现,准确量化裂缝的连通性是一项挑战。他们保守地估计了岩体的强度,假设裂缝已经完全穿透。这种方法虽然简单可行,但严重低估了岩体的强度。为了提高岩体的利用率,提出了二维裂隙连通性的概念。
研究人员最初将二维连接率定义为实测裂缝的平均轨迹长度等于贯通路径长度之和(裂缝的平均轨迹长度加上岩桥的平均长度)。然而,由于现场测量窗口大小的限制,获得裂缝的真实轨迹长度和岩桥之间的间距是极其困难的。窗口估计模型(H-H法),Wu等人根据测量窗口内可见、部分可见和不可见裂缝痕迹的比例估计连通性,显著解决了节理间距估计问题。此外,还提出了带宽投影法计算连通性,获得裂缝在剪切方向上的发育特征。带宽投影法假定岩体通常不是沿单个裂缝破坏,而是由分布在特定带宽内的多个裂缝控制。因此,2D连通性速率可以定义为假设投影基线上指定带宽内所有裂缝投影长度之和与投影基线长度之比。在尚未被破坏的岩体中确定投影计算的带宽仍然是一个挑战。尽管H-H法和带宽投影法都简单而优越,它们在三维分析计算中的适用性受到限制,因为它们没有考虑裂缝的三维空间特征。
根据二维连通性的定义,三维连通性是指裂缝在参考平面上的投影面积与参考平面面积之比。然而,目前的技术仍然无法精确表征裂缝面复杂的3D形态。为了获得裂缝的空间分布特征,利用物探、三维激光扫描、无人机摄影测量、图像分析等多种野外调查技术获取裂缝信息。然而,这些技术只捕获了浅层表面上一些发育的大裂缝的形态,并且所获得的连通性率的准确性一直存在争议。提出了FERM(岩体法医开挖)方法,通过向岩体中注入可膨胀化学剂来重建裂缝的三维形态,从而获得三维连通性率。该方法可以获得真实有效的裂缝连通性特征,但成本较高,不适用于大规模深部岩体裂缝。在过去的半个世纪里,基于统计的离散裂缝网络(DFN)建模方法逐渐成为获取裂缝三维连通性特征的主流方法。Priest等人首先提出使用计算机程序生成以数字或图形表示的不连续裂缝,随后被广泛应用于岩土工程。大量的实例研究表明,岩体中裂缝的几何参数(如形状、产状、迹长和密度)往往遵循一定的概率分布特征。蒙特卡罗裂缝网模拟可以根据所测道参数的分布模式对不确定性裂缝进行预测和模拟,通过增加模拟次数来解决构造真实裂缝网络图的问题。因此,确定裂缝的几何分布特征对于建立三维DFN模型至关重要。许多学者研究了裂缝的几何形状,假设DFN模型中的裂缝几何形状可以表示为薄圆盘或固定长宽比的四边形。在裂缝姿态表征方面,Fisher引入了基于围绕平均姿态旋转对称的二元Fisher分布。该分布只包含一个浓度参数,并且是可积的,因此应用广泛。然而,它最适合具有明确单峰浓度的数据集。当浓度参数较大时,分布的尾部衰减迅速,限制了其表示离群态度的能力。相比之下,Bingham分布在表示具有多模态或椭圆特征的数据时提供了更大的灵活性,因为它由对称矩阵控制。然而,它的应用需要复杂的数据处理和庞大的数据集来准确估计参数。对于三维DFN中的迹线长度和密度估计,Priest等人提出了不同的计算方法来估计平均迹线长度、空间维度和裂缝密度。
岩体内随机离散分布的裂缝在三维空间中相交,形成高度复杂的网络。尽管3D DFN建模技术已广泛应用于可视化裂缝的三维形态,并提供了计算三维连通性的基础模型,不同的研究人员提出了明显不同的参数化方法。此外,许多研究忽略了抽样偏差对模型精度的影响,使人们对所构建的DFN模型的可靠性产生怀疑。此外,目前计算三维裂缝连通性的方法通常会将定义区域内的所有裂缝不加选择地投影到参考平面上。这种方法不可避免地导致计算出的连通性与现场观察到的裂缝网络的实际穿过特性之间存在差异。总的来说,对于表征深部岩体中裂缝的三维分布和连通性,目前还缺乏系统有效的解决方案。
针对这些问题,本研究提出了一种基于裂缝面与采样面几何相交的裂缝采样偏差校正方法,从而构建更能反映裂缝系统空间特征的三维DFN模型。在此改进的三维DFN模型的基础上,首次应用A*算法在三维空间中识别潜在的穿过剪切面。这种方法可以选择不同海拔高度的关键裂缝,减少传统的基于投影的方法的局限性。将离散点插值与布尔运算相结合,提出了一种计算三维裂缝的新方法连接建立。该方法在西藏某水电站坝肩岩体低倾裂缝评价中得到了应用和验证。该方法有效解决了传统连通性计算的若干固有局限性,进一步拓展了三维DFN模型在剪切路径识别和裂缝连通性定量评价方面的应用潜力。为分析岩体裂隙的空间连通性特征提供了新的视角。
图表:
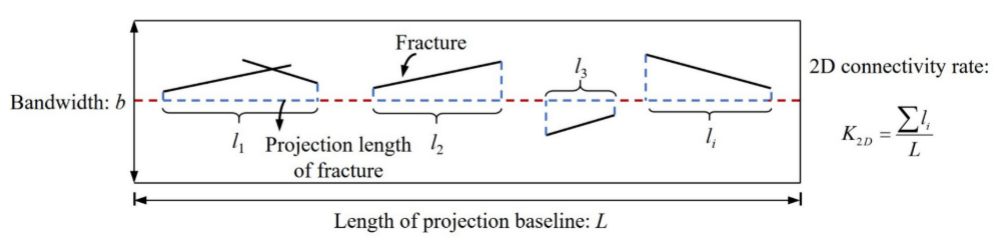
图1 二维连通性计算方法示意图
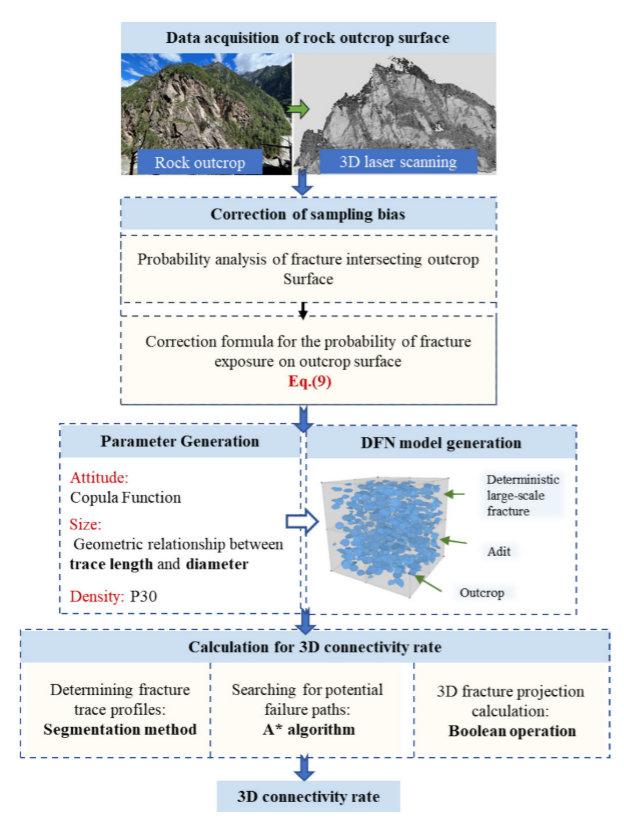
图2 三维裂缝连通性计算方法流程图
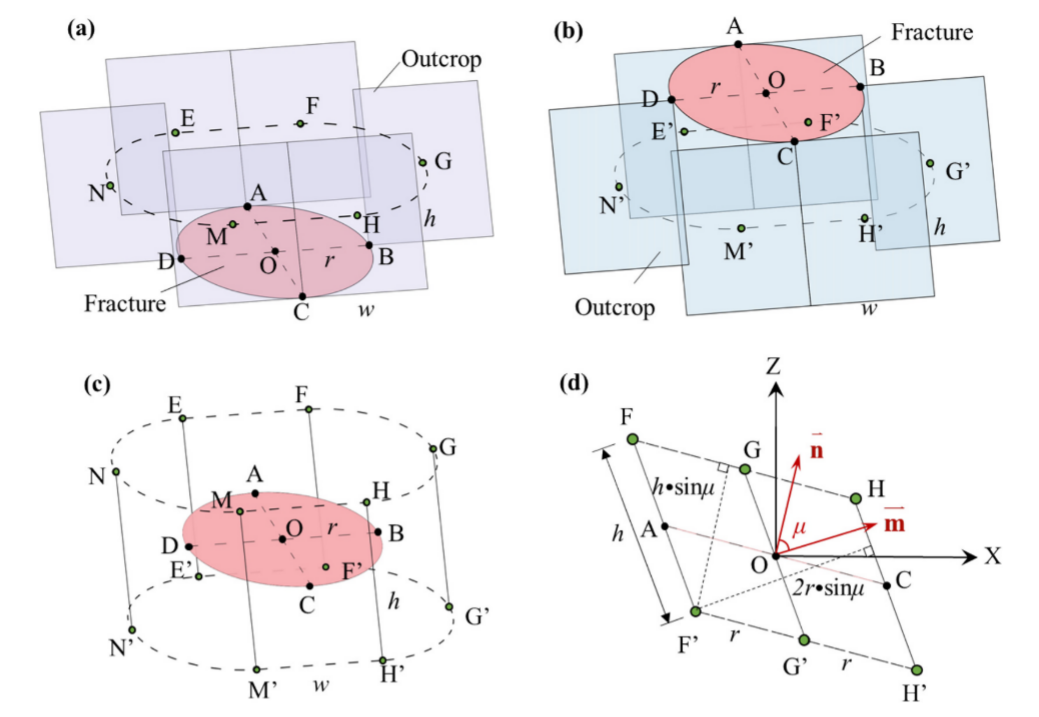
图3 裂缝与测量窗口的相交关系

图4 圆盘的中心、半径和轨迹长度之间的几何关系示意图
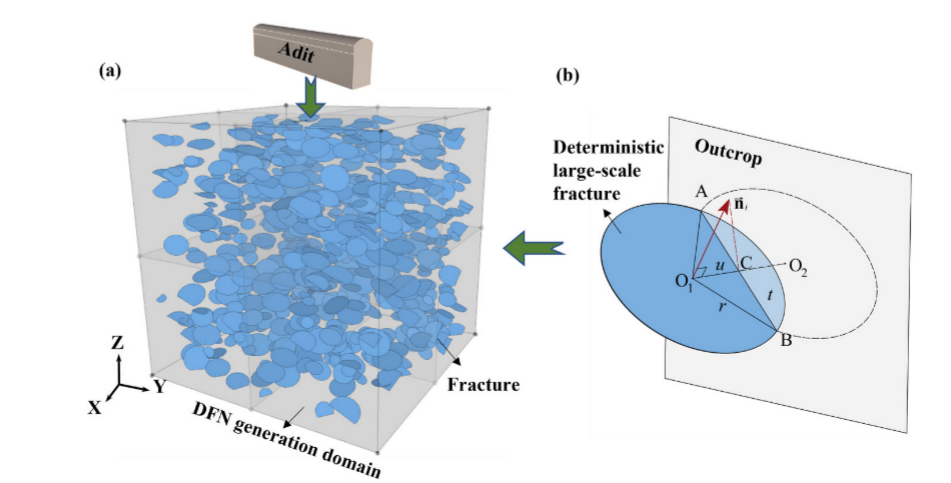
图5 DFN模型生成过程:(a)蒙特卡罗法生成DFN模型;(b)确定性大型裂缝坐标计算
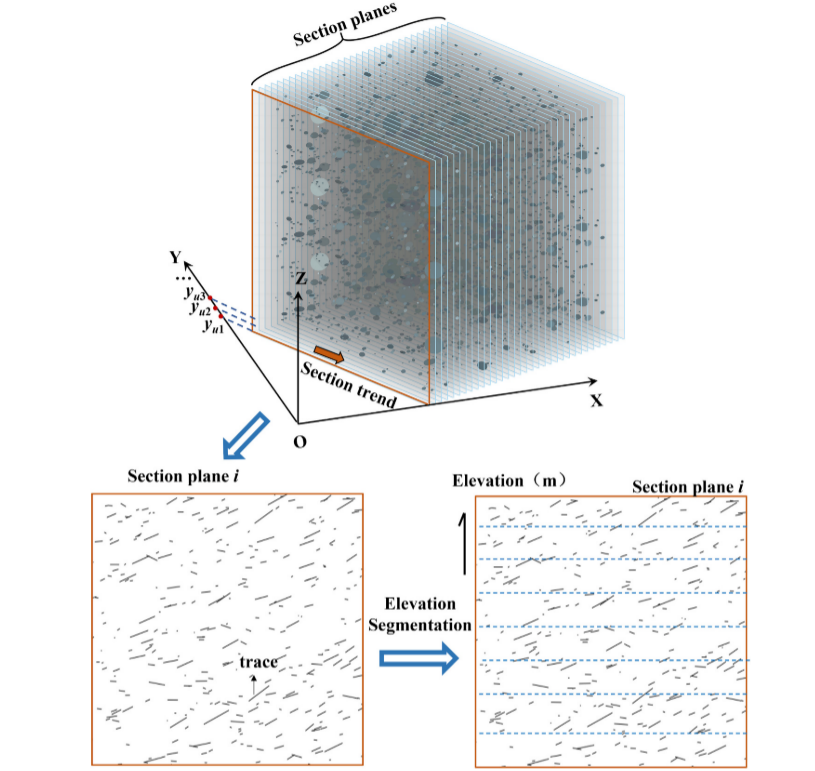
图6 DFN模型的二维轨迹生成过程
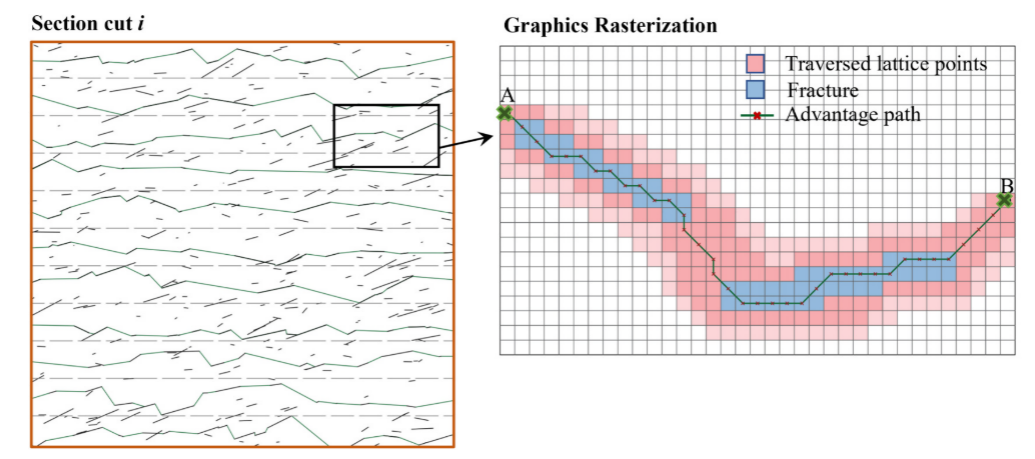
图7 A*算法搜索潜在故障路径的实现过程
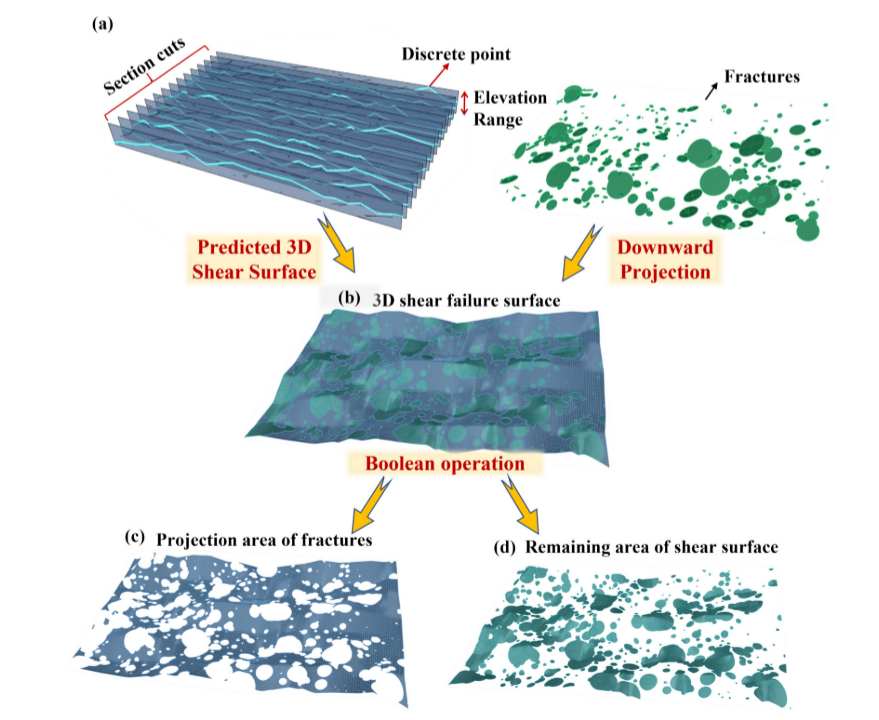
图8 三维剪切面生成过程:(a)空间离散点插值分析;(b)位势三维剪切面;(c)骨折投影面积;(d)剪切面剩余面积
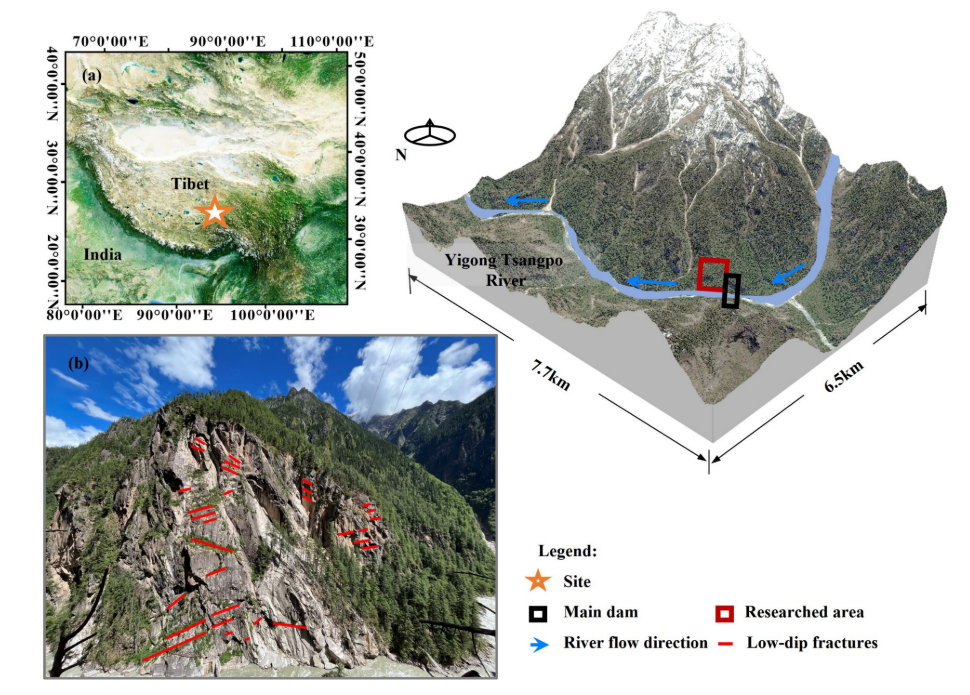
图9 研究领域的基本特征:(a)地理位置;(b)右岸坝肩现场照片
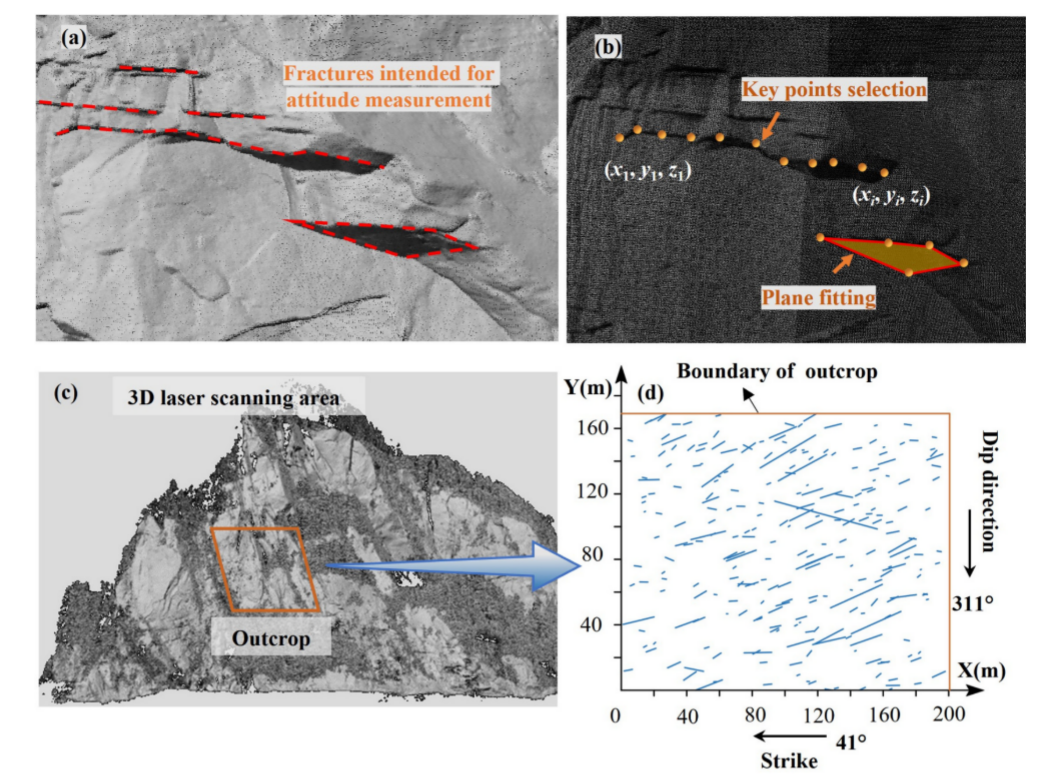
图10 裂缝信息获取流程:(a)裂缝面初始识别;(b)点云提取和平面拟合;(c)坡面三维激光扫描点云图;(d)裂缝迹线图
表1特殊情况下裂缝产状计算方法
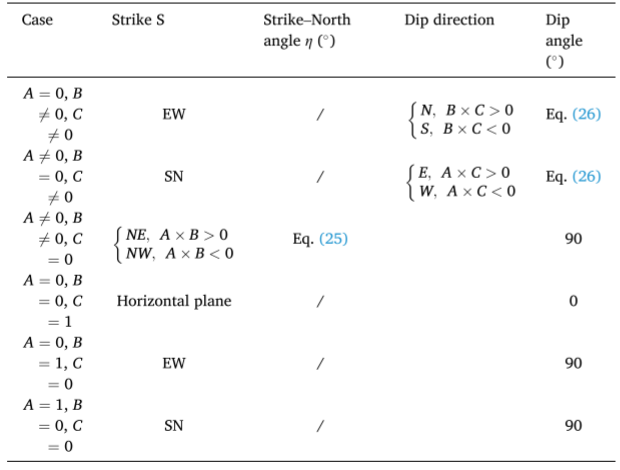
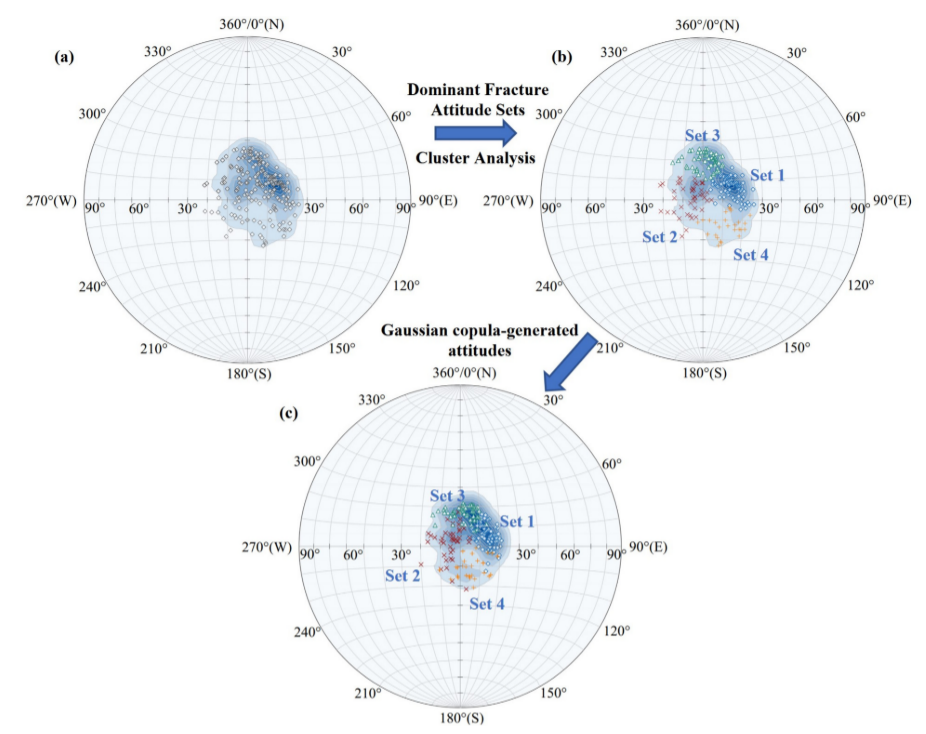
图11 裂缝极点立体轮廓图(Schmidt网):(a)现场测量结果,(b) K-means聚类结果,(c) copula模拟结果
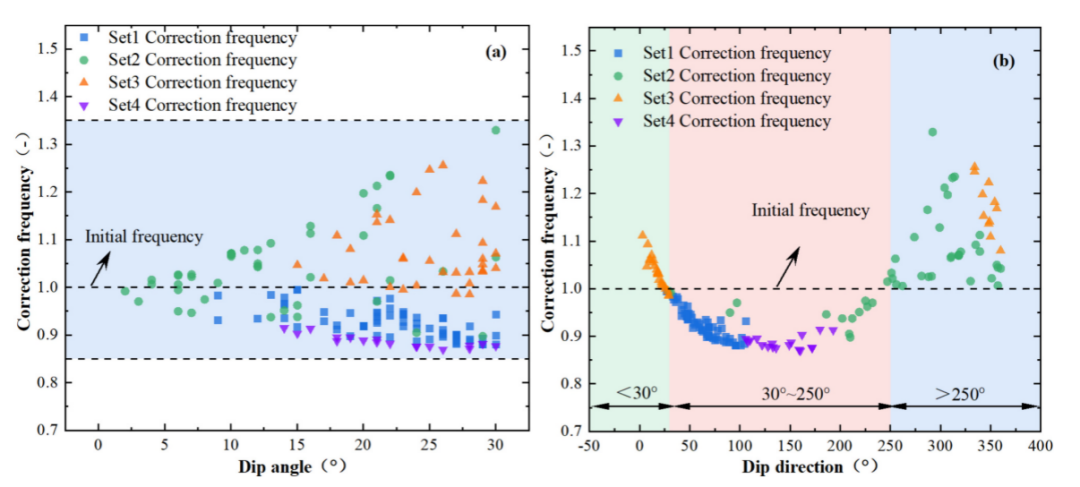
图12 裂缝采样频率校正结果:(a)校正频率与倾角散点图;(b)校正频率和倾斜方向散点图
表2 DFN模型低倾角裂缝基本参数

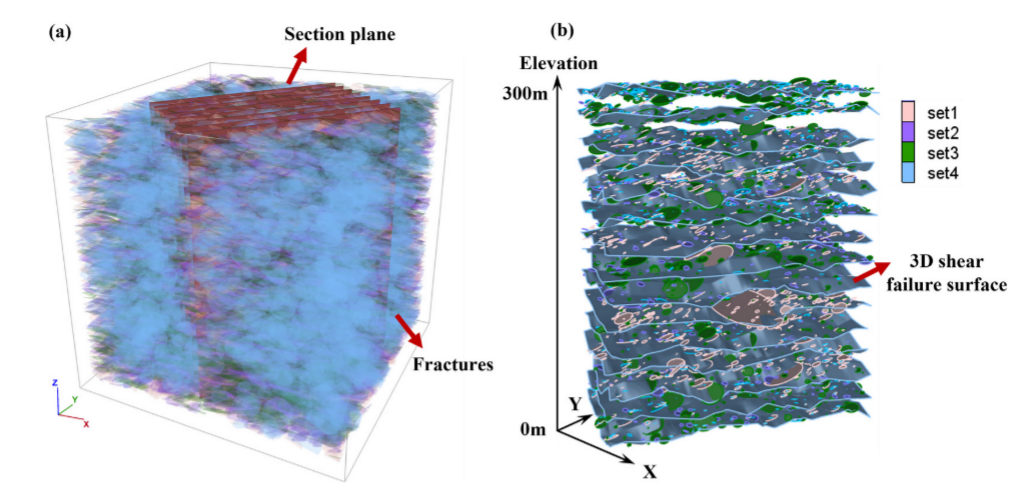
图13 低角度裂缝三维连通性计算过程:(a)三维DFN模型及计算截面;(b)潜在剪切面交点裂缝选择与投影计算
表3不同标高低角度三维裂缝三维连通性结果
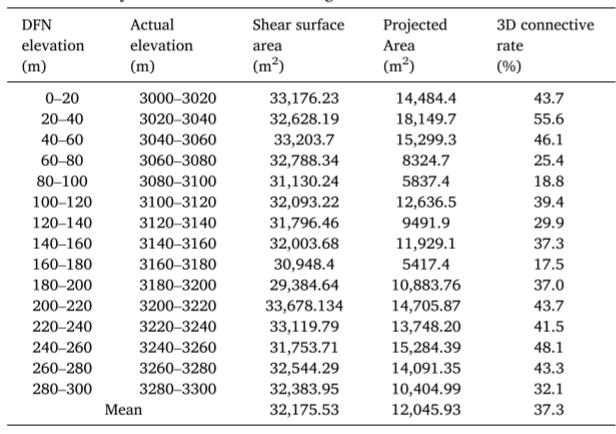
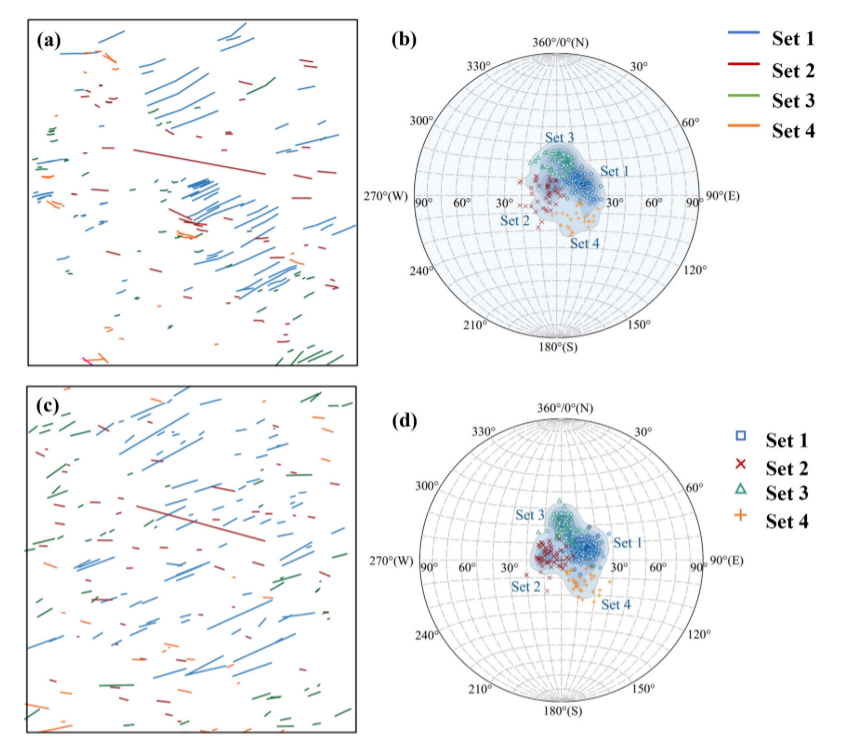
图14 野外露头与DFN模型露头的迹线和姿态比较
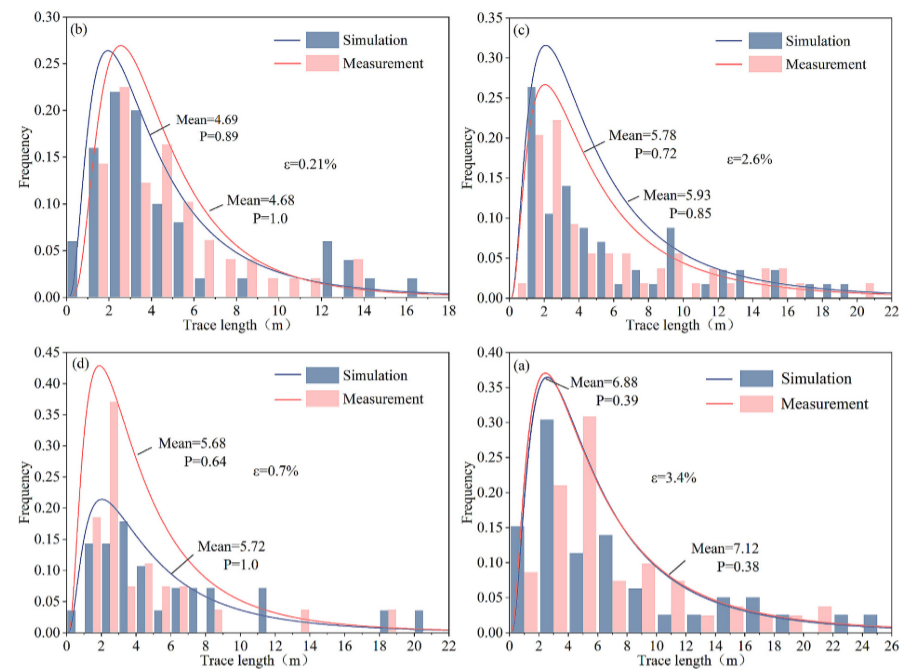
图15 DFN模型迹线长度与现场迹线长度的比较:(a)集合1;(b)组2;(c)组3;(d)第4组
表4 DFN模型走线长度与现场走线长度的偏差
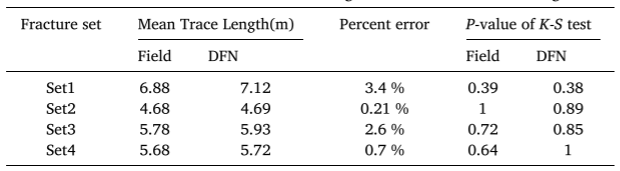
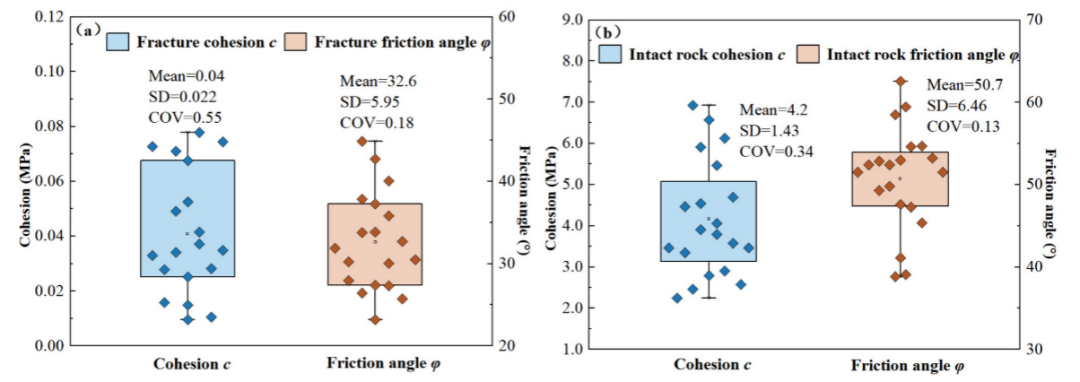
图16 抗剪强度参数箱线图:(a)断裂面;(b)完整岩石
表5岩石桥梁与裂隙力学参数取值

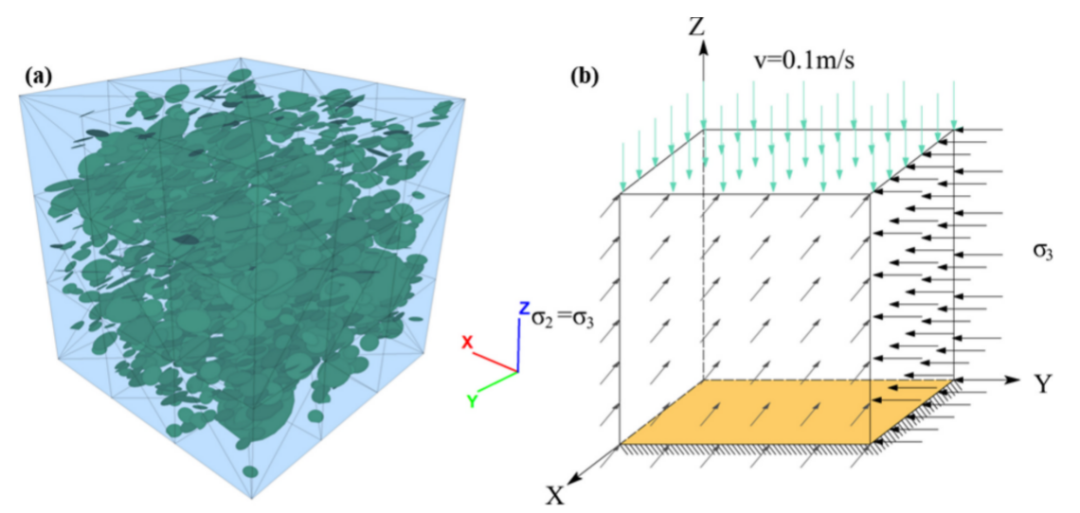
图17 数值模型及试验加载方法:(a)数值模型;(b)装载方式
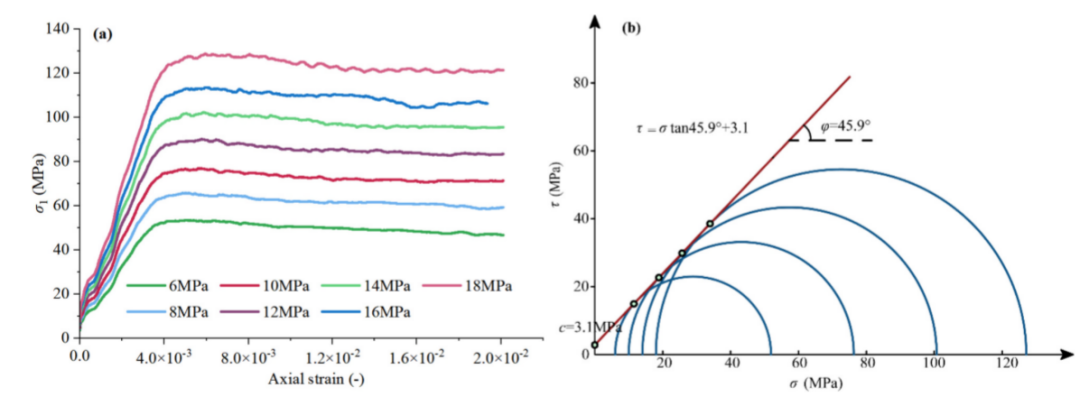
图18 不同围压和莫尔库仑强度包络线下的轴向应力-应变曲线:(a)不同围压下的轴向应力-应变曲线;(b)莫尔-库仑强度包络线
图19 右岸坝肩坑道低倾裂缝示踪图(局部视图)
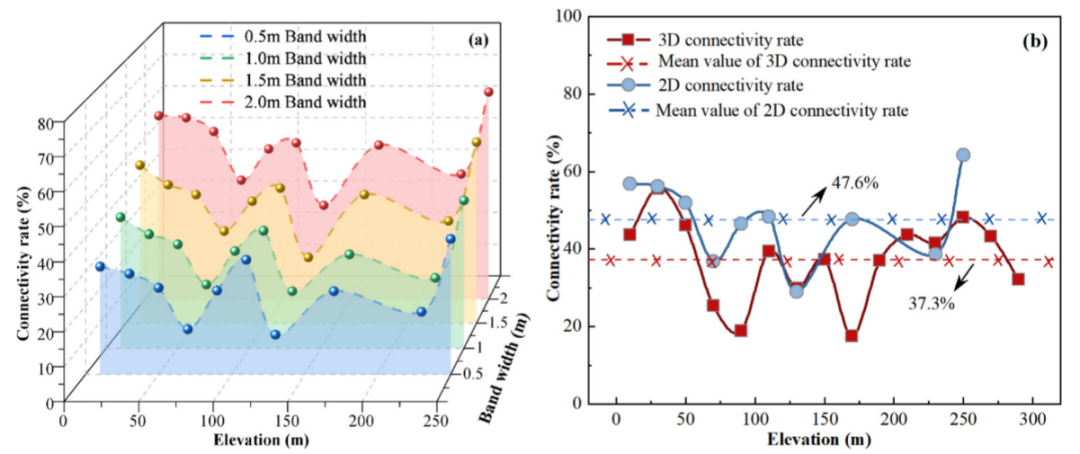
图20 坑道内低倾裂缝二维连通性计算结果:(a)不同带宽下二维连通性计算结果;(b)二维与三维连通性计算结果对比
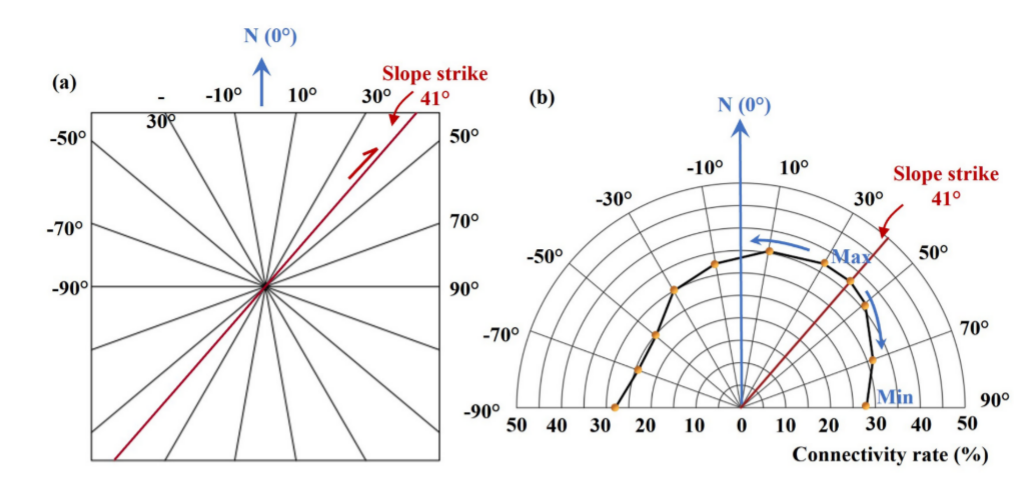
图21 裂缝连通性的方向敏感性分析:(a)切片方向示意图。(b)不同剪切方向下连通性玫瑰图
表6不同剪切方向连通性及稳定性计算结果

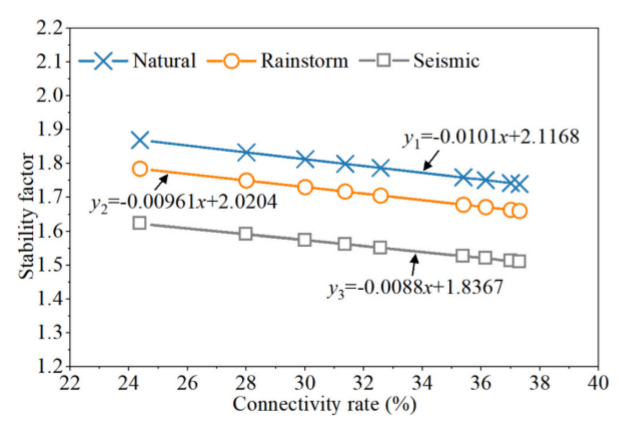
图22 连通性与稳定性因子的关系
结论:
研究了岩体中裂缝的空间连通性特征,提出了一种计算三维裂缝连通性的新方法。本研究的主要贡献总结如下:
(1)提出了基于裂缝与露头面相交概率的裂缝采样频率修正模型,为后续三维连通性计算提供了可靠数据。
(2)引入联结二元分布函数来表示裂缝走向与倾角之间的相关性,克服了传统方法单独处理这些参数的局限性。
(3)利用统计建模参数和修正后的裂缝频率,建立了包含确定性大尺度裂缝和露头的更精确的三维DFN模型。A*算法结合离散点插值分析预测潜在的三维剪切面,布尔运算进行三维投影计算裂缝涉及潜在的破坏路径,从而产生更精确的三维连通性计算方法。
(4)将该方法与传统的二维计算方法相结合,对西藏某水电站坝肩岩体低倾裂缝连通性进行了评价。连通性结果分别为37.3%和47.6%。与机械反分析得到的值(32.5%)相比,该方法产生的偏差仅为4.8%,显示出更高的精度。
(5)三维连通性计算方法具有方向敏感性,连通性随剪切方向与边坡走向夹角的增大而增大。这种行为受到边坡中主要裂缝产状的影响,并突出了不仅根据几何形状,而且根据岩体的地应力条件选择剪切方向的重要性。
参考文献
[1]Liang P, Wei Y, Guo H, et al. 3D connectivity calculation method for low-dip fractures in high-steep rock slopes[J]. Engineering Geology, 2025, 355: 108227.
 成功提示
成功提示
 错误提示
错误提示
 警告提示
警告提示
评论 (0)