2025-09-23 2028 0

摘要: 光滑粒子流体动力学(SPH)是一种基于粒子的拉格朗日数值方法,特别适用于模拟具有不同本构方程流体的自由表面流动。本研究开发了一种SPH模型,用于求解稠密状态下颗粒物质的流动问题,该模型采用了Pouliquen等人与Jop等人提出的本构方程。 通过引入颗粒的弱可压缩性,解决了静态条件附近流动解析的难题:该方法需通过求解三阶代数方程来计算颗粒材料密度。针对具有可变屈服应力的任何粘塑性流体,本研究开发了一种新的粘度正则化方法,以实现流动停止与静态条件的精确再现。通过求解解析解已知的均匀颗粒流动问题,并复现Lube等人关于颗粒柱坍塌的实验数据,完成了对该模型的验证工作。 引言: 自由表面流动的数值模拟通常是一项复杂任务——尽管过去已成功提出如流体体积法等基于网格的方法,但无网格粒子方法似乎为处理自由表面问题提供了更有效的途径。在各类粒子方法中,光滑粒子流体动力学(SPH)已被证明具有广泛适用性。该方法最初由Gingold与Monaghan以及Lucy提出用于天体物理应用,后经Monaghan、Ferrari等人以及Violeau和Issa等学者应用于自由表面流动模拟。 SPH方法在实现不同本构方程方面具有显著优势:Rodriguez-Paz与Bonet、Laigle等人、Pasculli等人以及Minatti与Pasculli采用Bingham类流体实现泥石流的SPH模拟,而Bui等人则运用弹塑性关系模拟土体破坏流动。关于SPH方法的全面综述及应用实例可参阅Monaghan、Liu与Liu以及Violeau的论著。 本研究旨在利用SPH方法的上述特性,开发用于模拟复杂自由表面稠密颗粒流动的数值模型。颗粒流动在工业领域具有广泛应用,从制药到半导体行业(根据Richard等人的研究,颗粒材料是仅次于水的第二大被处理材料),同时在土木工程领域也备受关注:近年来,极端事件中河流携带固体材料造成的灾害风险日益受到重视。 目前科学界尚未建立适用于所有流动类型的通用颗粒物质本构方程。然而,现有研究已提出多种本构方程,其中每一种都能准确再现特定类别的颗粒流动现象。当前研究重点关注Pouliquen等人与Jop等人提出的本构方程,该方程可适用于稠密状态下以摩擦作用为主导的广泛颗粒流动类型。 本文提出的SPH模型采用了一种新型压力计算方法,该方法对于解决低变形应变率下的流动问题至关重要。该方法的创新之处在于引入了颗粒的弱可压缩性特性,并专门针对所研究的本构方程体系进行了优化。此外,该SPH模型还具有新型粘度正则化方法的特点,适用于任何具有可变屈服应力的粘塑性流体。 第二章将阐述描述系统物理过程的控制方程及其所采用的本构方程;第三章提供SPH方法的总体框架;第四章详细介绍所提出的SPH模型;第五章通过复现已知解析稳态解的简单表层流动试验案例,以及重现Lube等人的颗粒材料坍塌实验测量数据,完成对模型的验证工作;最终第六章就模型及其性能表现给出结论性评述。 图表:
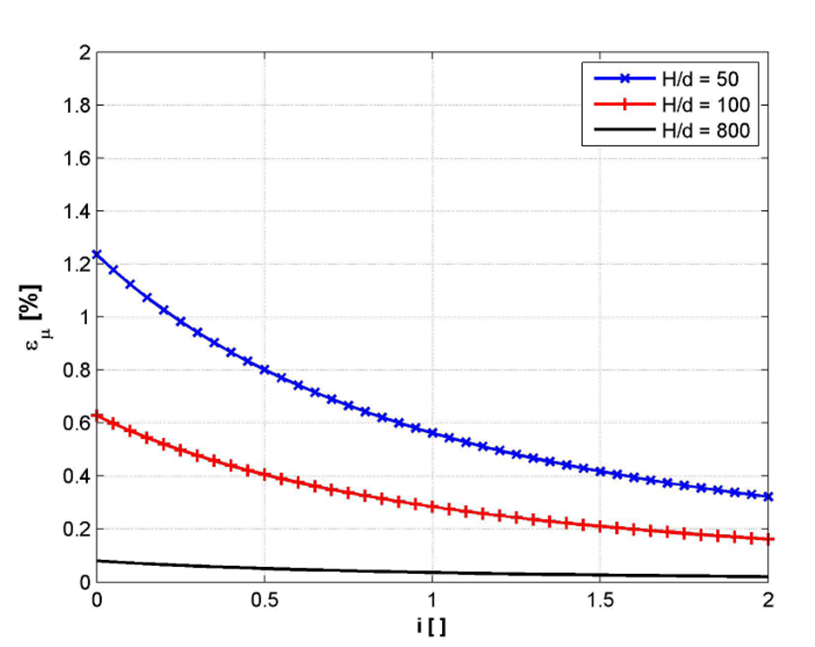
图1:忽略公式18中2.61d/H项所产生的相对误差随i的变化关系曲线。所有曲线均在µ2/µs ≈ 1.5 和 i0 = 2.65 的条件下绘制。
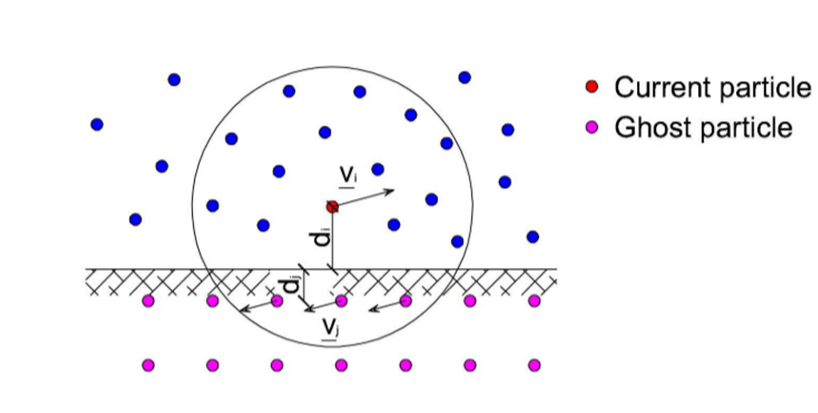
图2:Morris等人提出的虚拟粒子方法示意图。
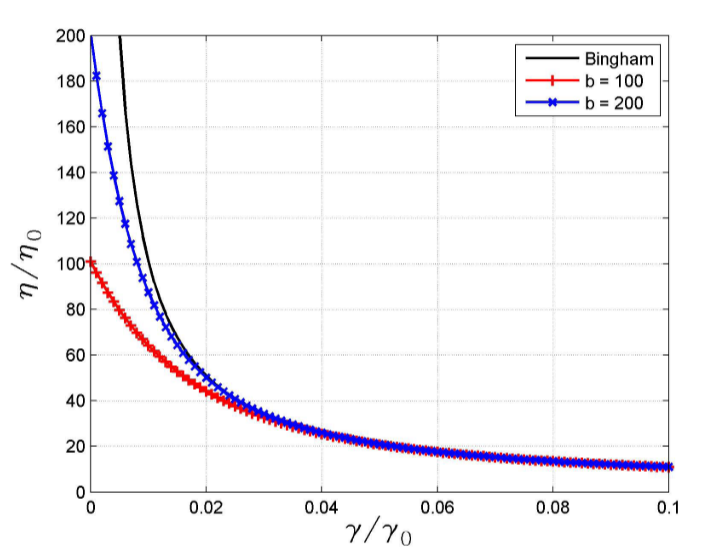
图3:根据公式45和46,精确Bingham模型与Papanastasiou模型的粘度-应变率关系曲线。图中˙γ0 = τy/η0, mp = b/˙γ0。
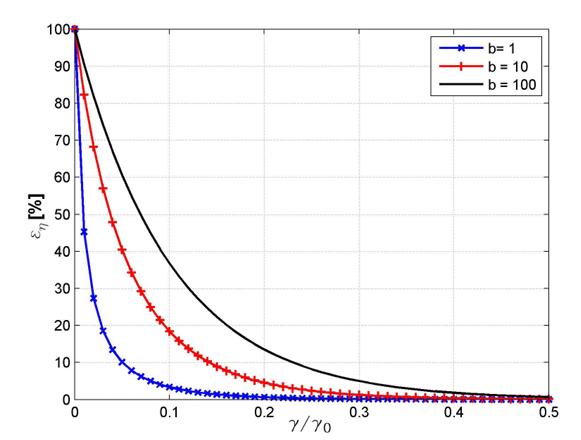
图4:本研究本构方程采用Papanastasiou方法正则化粘度的相对误差曲线。三条曲线的差异在于屈服应力τy的取值,该值被设置为比单位标度应力τ0(τy = bτ0)大b个数量级。参数mp的选择使得在剪切率˙γ = 0时,粘度值比残余粘度η0大一个数量级。
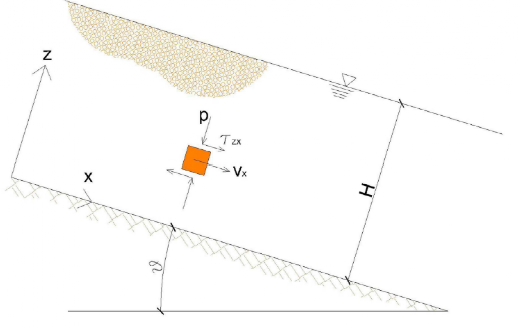
图5:均匀颗粒流沿斜面向下流动示意图。
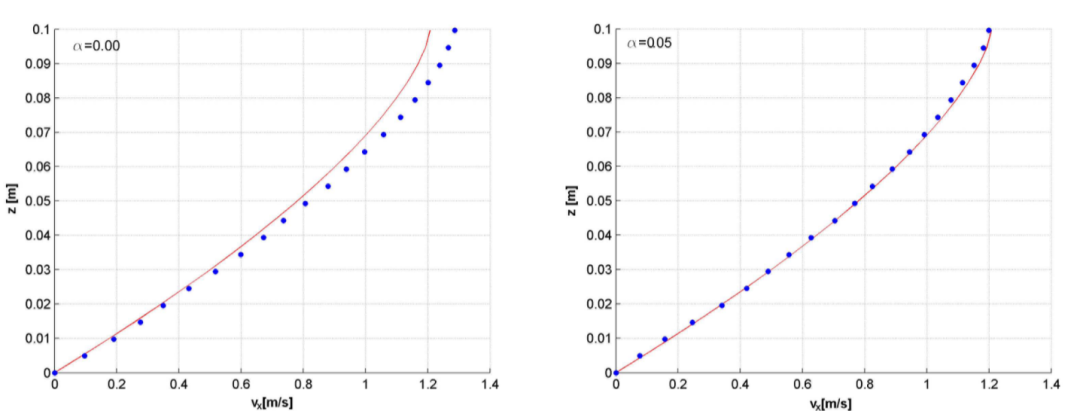
图6:模拟颗粒流沿斜面向下流动的稳态速度分布图。连续线代表解析解。左图未使用人工粘度(α = 0),右图采用了α = 0.05的人工粘度。两种情况的稳态均在模拟时间约6.50秒后达到。
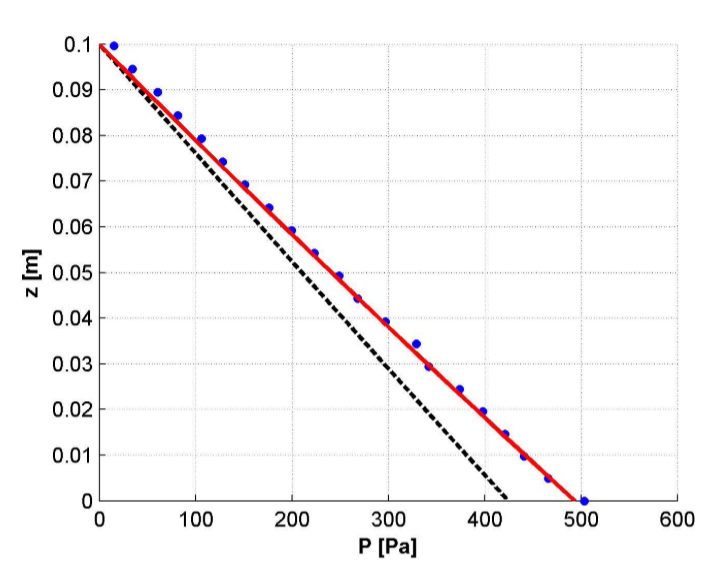
图7:模拟颗粒流沿斜面向下流动的稳态压力分布图。虚线表示不可压缩颗粒的解析解,实线表示采用状态方程的可压缩颗粒解析解。本次模拟未使用人工粘度(α = 0)。
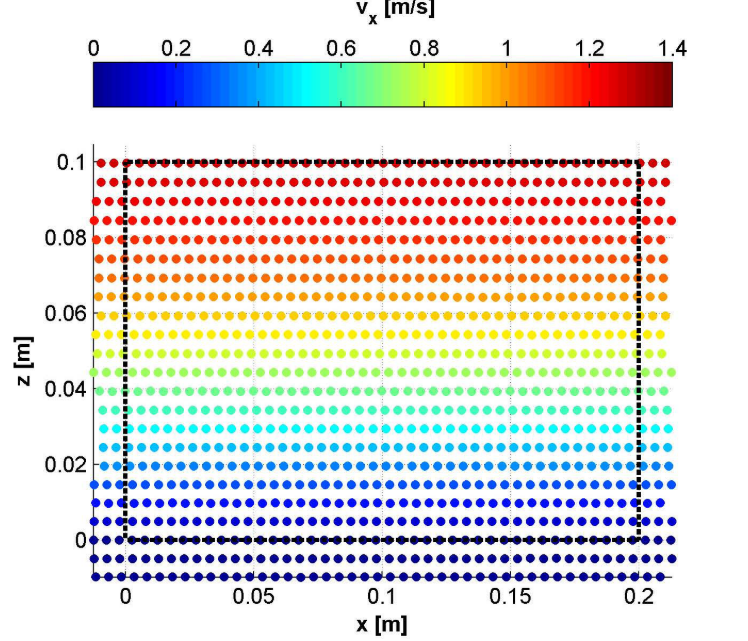
图8:颗粒流沿斜面向下流动的稳态粒子分布图。粒子按vx值进行颜色编码,黑色虚线标示流体流动区域。线下粒子为边界粒子,侧边粒子是为实现周期性边界条件而复制的标准粒子。
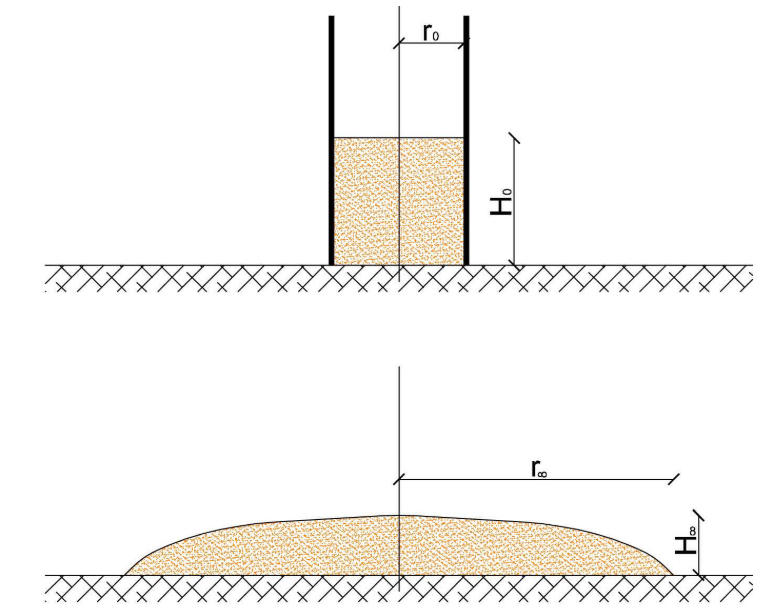
图9:颗粒柱坍塌实验装置与参数定义示意图。
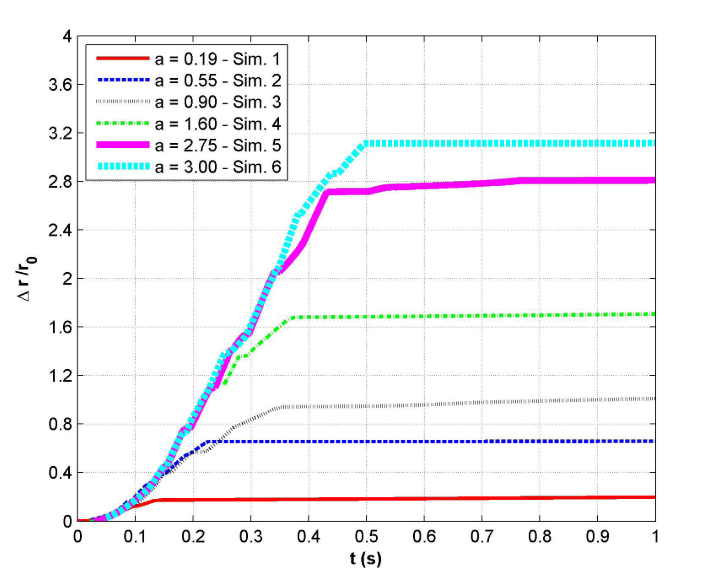
图10:颗粒柱坍塌模拟的前缘位置-时间关系图。∆r表示前缘相对于柱体坍塌前初始位置的推进距离。
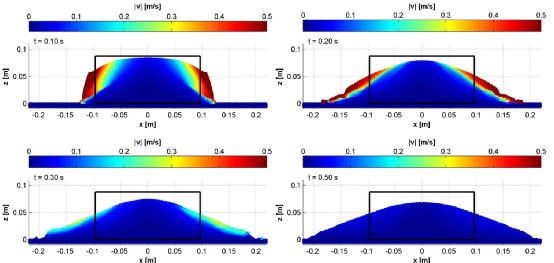
图11:a = 0.90条件下颗粒柱坍塌模拟的粒子分布图。粒子按速度模值进行颜色编码,各图均标注模拟参考时间。黑色边框用于追踪堆积体的初始形态。
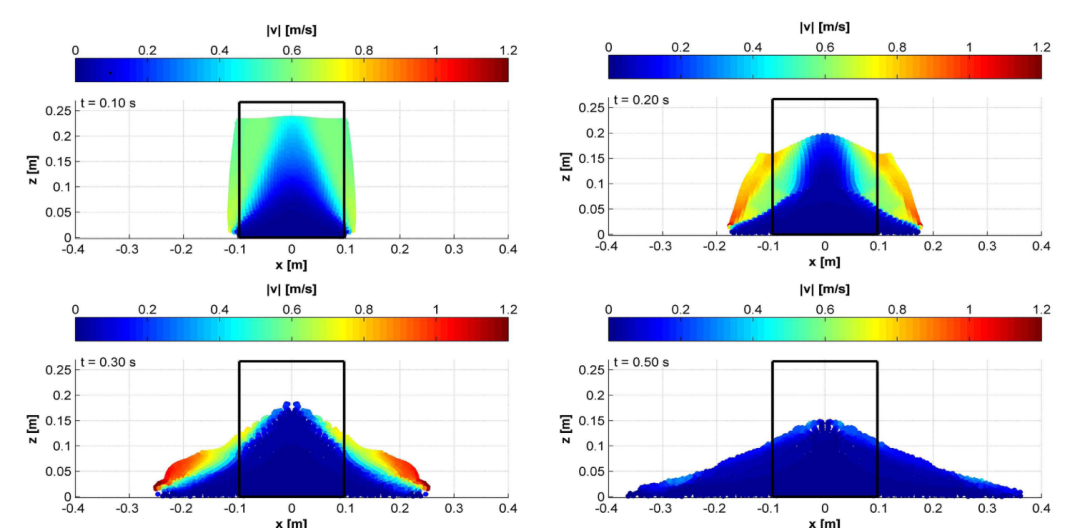
图12:a = 2.75条件下颗粒柱坍塌模拟的粒子分布图。粒子按速度模值进行颜色编码,各图均标注模拟参考时间。黑色边框用于追踪堆积体的初始形态。
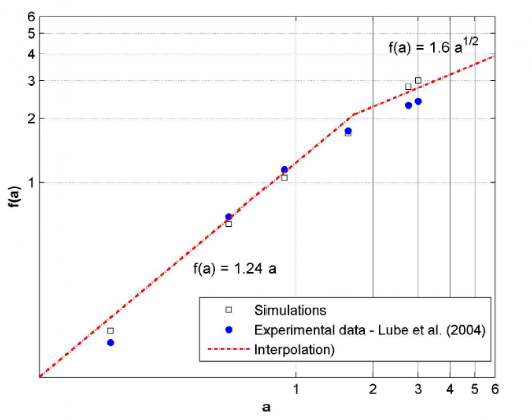
图13:沙粒柱坍塌数值模拟标度律与Lube等人实验标度律的对比。
结论: 本文提出了一种用于求解稠密状态下颗粒流动问题的SPH模型。该模型采用Pouliquen等人与Jop等人提出的本构方程,该方程专门针对稠密流动状态而建立。研究采用弱可压缩SPH方法(WCSPH),该方法能有效反映本构方程的特性——该方程预测随着流动强度增加,颗粒堆积密度将逐渐减小。 为解决近静态条件下出现的压力估算问题,必须引入颗粒的弱可压缩性特性。这一举措使得问题中新增了未知量,算法需要在每个时间步长对每个粒子求解三阶代数方程,以此计算颗粒材料的密度。 本文提出了一种新型粘度正则化方法,用于模拟近静态及流动停止工况。该方法适用于任何具有可变屈服应力的粘塑性模型,并通过求解一阶常微分方程来计算正则化粘度。实践证明,该方法能以合理精度有效再现近静态及流动停止状态。 通过将模拟结果与倾斜平面上均匀流动的解析解进行对比,并复现Lube等人的颗粒柱坍塌实验数据,对该SPH模型进行了验证。在稠密流动状态下,模型的计算结果与已知解析解及观测数据吻合良好,证明该模型能有效处理本构方程的各项特性,如空间变化粘度、压力相关屈服应力以及静态条件下的奇异行为。 关于模型的扩展应用,未来可通过引入适用于碰撞流态的本构方程进行升级——在该流态中颗粒间距较稠密状态更大,且流动强度通常更高。针对更大高宽比a值的工况,仍可采用Lube等人的实验数据对模型进行验证。 参考文献:
Hot News
 成功提示
成功提示
 错误提示
错误提示
 警告提示
警告提示
评论 (0)